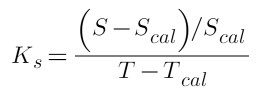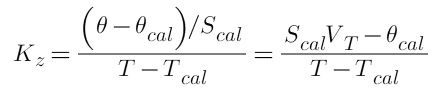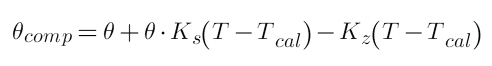Environmental temperature changes alter the mechanical and electrical characteristics of all instrumentation. Metals expand and contract, and electrical properties such as resistance and capacitance rise and fall. These effects change instrument output and lessen the accuracy of the measured variable (pressure, flow, tilt, strain, etc.). This technical note describes the source of temperature dependence in one type of instrumentation, Jewell Instruments electrolytic tiltmeters, and explains how to remove this effect to maximize accuracy. The principles presented here also apply to many other instrument types.

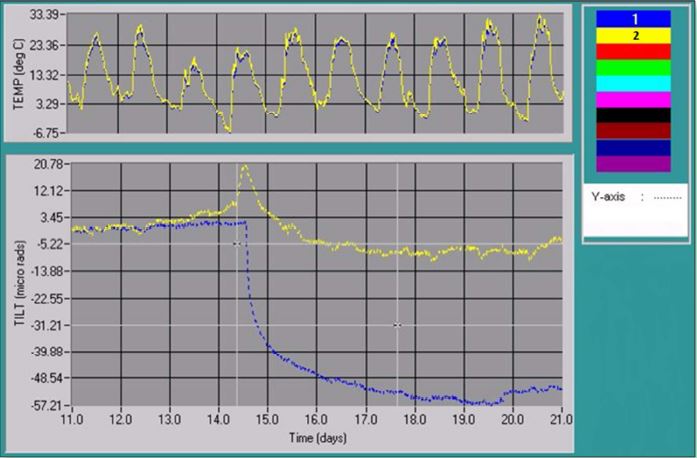
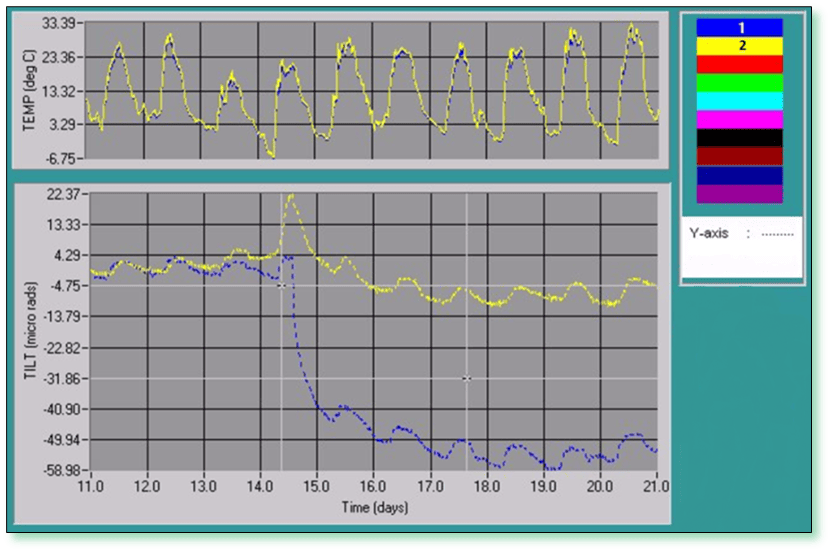
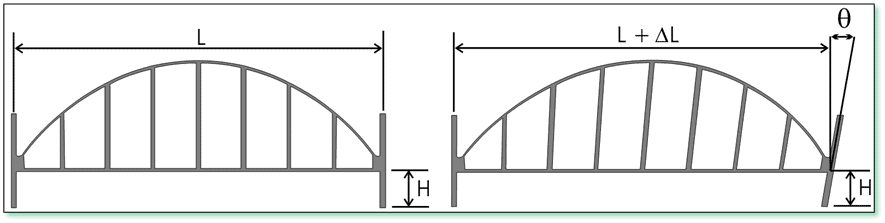
Just as instrumentation exhibits temperature-dependent behavior, so too do natural and engineered structures including slopes, embankments, and concrete and steel construction. Thermal expansion and contraction in response to daily and seasonal temperature fluctuations generate real movements that are detected by tiltmeters and other sensors. The magnitude of this effect, and ways of differentiating it from purely instrumental behavior, are discussed in this article.

Sources Of Temperature Coefficients

Figure 1: Electrolytic Sensor

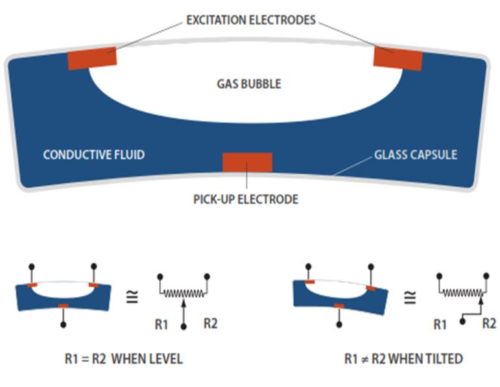
The sensors in Jewell Instruments Geotech/Tech tiltmeters are known as electrolytic tilt sensors, a type of electronic spirit level comprised of a glass case and containing a conductive liquid (electrolyte), an air bubble, and platinum electrodes. As the sensor tilts, the wetted area of each excitation electrode increases or decreases, depending on the tilt direction. This change causes the electrical resistance between the central pickup electrode and each excitation electrode to rise or fall. It is these resistance changes that are sensed by the tiltmeter electronics, which convert them to precise measurements of the magnitude and direction of tilt.

Temperature fluctuations cause thermal expansion and contraction of the sensor liquid, shrinking or swelling the air bubble and changing the amount of liquid in contact with each excitation electrode. This process alters the scale factor (gain) of the sensor and can shift its zero point. Small changes in sensor output in the absence of any real tilt movement are the result. Experiments have shown that volumetric expansion and contraction of the liquid is the single biggest source of temperature coefficients in Jewell Instruments electrolytic tiltmeters. This effect is much greater than dimensional changes of the sensor’s glass case, which has a thermal expansion coefficient 100 times smaller than that of the liquid.

Thermoelasticity of the tiltmeter housing, and of the mechanical connections between housing and sensor, is another source of tiltmeter zero shift. To minimize this effect, rigid housings are used and connections between the sensor and enclosure are made as few as possible. In many designs we pot the tilt sensor directly into the housing base, eliminating mechanical connections entirely and turning the sensor and base into one unified element.

The temperature effects described above are partially removed (compensated) by the tiltmeter’s electronic circuitry. The apparent tilt (residual error) remaining after such compensation is highly repeatable and is described by two linear temperature coefficients, the temperature coefficient of scale factor, KS, and the temperature coefficient of zero shift, KZ. These coefficients include contributions from all sources, including the tiltmeter electronics.

There is one additional effect of temperature on electrolytic tilt sensors. The conductivity of the electrolyte changes more than five-fold over the typical operating range of a tiltmeter (typically -40°C to +70°C). By measuring sensor output ratiometrically (taking output as a percentage of input), Jewell Instruments electrolytic tiltmeters remove this effect entirely. However, in designs that incorporate the sensor as part of a Wheatstone bridge, electrolyte conductivity change can be a major source of measurement error.

Temperature Coefficients Defined

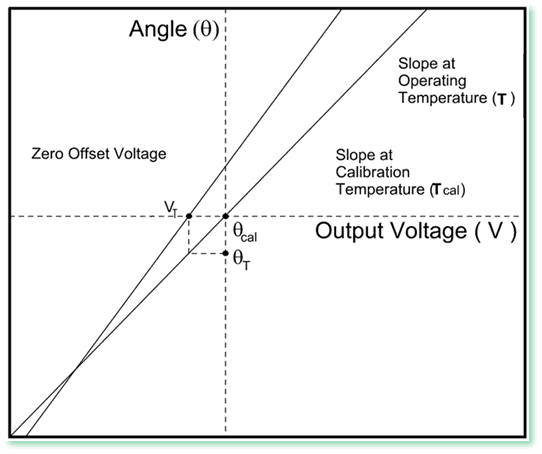
Scale factor is the proportionality constant between tilt angle and tiltmeter output. It is determined in the factory by calibrating the tiltmeter – rotating it through a range of known angles and recording the output voltage at each angle. The slope of the best-fit straight line through the calibration data is the scale factor Scal that is reported on the tiltmeter calibration certificate. In reality, the slope is slightly different at each temperature.

Equation 1:

Figure 2: Calibration lines at two different temperatures, Tcal and T.

The change of slope per unit temperature change is the temperature coefficient of scale factor where Scal is the scale factor at the calibration temperature Tcal, and S is the scale factor at a different temperature T.

The temperature change can also shift the zero crossing of the calibration line in the absence of any real tilt of the structure to which the tiltmeter is attached. In the graph, the zero offset voltage is VT which leads to an apparent tilt angle of q = ScalVT at temperature T. The zero shift is therefore q – q cal or ScalVT – q cal. The zero shift per unit temperature change is defined as the temperature coefficient of zero shift, Kz.

Equation 2:

The coefficients KS and KZ are determined in the laboratory by performing calibrations at two or more temperatures and include contributions from all sources. Their values are specific to each of the several classes of tiltmeters made by Jewell Instruments and are available on request. For tiltmeters with the designation “high gain,” the ones most typically used in geotechnical engineering, KS @ +0.0004/°C and KZ @ 1.5µradian/°C (= 0.2 arcsecond/°C). Temperature coefficient values should decline in the future as sensor and electronic designs advance.

Equations For Temperature Compensation

Equation 3:

For uncompensated tiltmeter measurements, the tilt angle q is simply q = S_calV where V is the measured voltage and S_cal is the scale factor measured at the calibration temperature T_cal. For measurements at all temperatures, S_cal, the scale factor is first adjusted using the temperature coefficient K_Sbefore computing q.

Equation 4:

The zero offset is then removed using the temperature coefficient Kz and the true compensated tilt angle qcomp is computed using Equation 5. Where

Equation 5:

q_comp	= true angular position (tilt)
T	= the temperature at which your measurement was made
T_cal	= the calibration temperature reported on the tiltmeter calibration certificate
S	= scale factor at temperature T
S_cal	= the scale factor reported on the tiltmeter calibration certificate
V	= the measured output voltage at temperature T

Equation 6:

Inserting Equation 4 into Equation 5, and expanding results in Equation 6.

Recognizing that S_calV is the uncompensated angle q, we can rewrite Equation 6 as
q _comp= q + q • K_s( T – T_cal) – K_z( T – T_cal).

Equation 7:

Equation 7 intuitively shows the compensation of the angular measurement consists of the uncompensated angular measurement, a slope compensation term that scales the uncompensated angular measurement and a zero offset term that is dependent on temperature only.

Finally, this temperature compensation procedure is an option for all Jewell Instruments electrolytic digital tiltmeters. It may also be incorporated into spreadsheets and other user-written programs.

Thermoelasticity In Geotechnical Engineering

Thermoelasticity is the elastic expansion and contraction of materials in response to changing temperature. Soil, steel, and concrete structures each have their own temperature coefficient, the coefficient of thermal expansion µ, which is expressed in units of strain (microinches per inch or microns per meter) per unit change in temperature. Thermoelasticity is a major source of structural movement, and precision tiltmeters easily measure this behavior. Thermoelastic deformation typically produces tilts that exceed the temperature-induced output changes of properly designed tiltmeters. The following example illustrates the effect of large thermoelastic movements.

Tiltmeters are commonly installed on bridge piers and columns to detect early signs of settlement and riverbed scour. The bridge above on the left shows a bridge with one span. Let us assume that the span is fixed at one end but can expand laterally at the other. Now if the slip bearings are seized at the movable end, thermal expansion of the span by an amount DL will result in a tilt of the right pier of q=sin^-1(DL/H). If the temperature change is 10°C, µ is 10^-5/°C and span length L is 30 meters, then: DL = (10°C)( 10^-5/°C)(30,000 mm) = 3 mm.

For a pier that is 3 meters high, the tilt will be: q = 1000 microradians = 206 arc seconds.

Now compare this 1000 microradian movement with the uncorrected temperature-induced error of a Jewell Instruments electrolytic tiltmeter. Our “high-gain” tiltmeters, typically used in geotechnical and structural monitoring, have temperature coefficients of K_S @ 0.0004/°C and K_Z @ 1.5 microradians/°C. A 10°C temperature change, therefore, produces a zero shift of 15 microradians, 1.5% of the actual pier movement. The error induced by the coefficient K_S is proportional to the rotation angle of the tiltmeter and the temperature change and is even smaller. If the tiltmeter was leveled (nulled) during installation, its angle after column rotation would be 1000 microradians and the K_S error would be (0.0004/°C)(10°C)(1000 microradians) = 4 microradians.

In this example the tiltmeter measures thermoelastic tilt of the pier to better than 2% accuracy with no temperature compensation. Compensating the readings for temperature change yields improved results. Although this is a hypothetical example, it is typical of real field projects involving Jewell Instruments electrolytic tiltmeters. Most of the correlation of tilt with temperature results from thermoelastic deformation. If your data still correlate with temperature change after compensating for temperature, you are observing real structural or ground movement.

How To Minimize Temperature-Induced Measurement Errors Without Temperature Compensation

There are several ways to minimize temperature-induced measurement errors that do not involve any data processing at all. In many cases, these methods eliminate the need for the temperature compensation procedures outlined above.

Reduce Temperature Extremes. When possible, instruments should be installed underground or in shaded locations where temperature extremes are minimized. If temperatures do not vary, they can have no effect on your measurements. If your instruments must be installed in locations exposed to direct sunlight, set up a hood that keeps them shaded while maintaining good ventilation.

Choose Light Colors. When other specifications are equal, light-colored instruments stay cooler and are preferable to dark-colored ones.

Establish Your Accuracy Requirements. Before selecting the tiltmeters for your project, decide on the accuracy that is required and estimate the temperature range that the instruments will experience. Then get temperature coefficients for the tiltmeters under consideration from their manufacturers. Use the temperature range and coefficients to compute potential errors, following the procedure in the previous section. If these errors are smaller than your accuracy requirements, no temperature compensation is necessary.

Use a Mechanically Stable Tiltmeter Design. Choose a tiltmeter design that minimizes thermoelastic deformation of the instrument itself. Compact, stiff housings are more stable and less likely to bend or vibrate than elongated beam designs with fixed ends. Also, the fewer the mechanical linkages between internal sensor and outer enclosure, the better.

Use a Mechanically Stable Mounting Method. Use a mounting method that maximizes thermoelastic stability. Three-point mounting is best because it is the most rigid and prevents bending and torsion that can occur with 2-point mountings. Mounting studs (typically threaded rods) that attach the tiltmeter to the structure should be as short as possible, of the same length and of the same material. In special cases thermally stable, but more expensive, invar studs can be used.

Conclusions

All instruments exhibit some degree of temperature-dependent behavior. Thermal expansion and contraction of the sensor liquid is the largest source of temperature dependency in Jewell Instruments electrolytic tiltmeters.

The effect of temperature change on tiltmeter output is predictable and repeatable. It is quantified by two constants, the temperature coefficient of scale factor, KS, and the temperature coefficient of zero shift, KZ. These constants enable the user to predict the magnitude of potential temperature-induced errors and to correct (compensate) for such errors during data analysis.

The large thermoelastic movements of civil engineering structures are easily detected by tiltmeters and are sometimes mistaken for measurement errors.

Before beginning an instrumentation project, the user should first establish the required measurement accuracy then estimate the measurement error over the expected temperature range using the instrument’s temperature coefficients. If the error is smaller than the accuracy requirements, then no temperature compensation is necessary.

Simple precautions such as installing tiltmeters in the shade or underground can reduce or eliminate temperature effects.

Temperature compensation of Jewell Instruments electrolytic tiltmeter readings is performed using Equation 6 or Equation 5 if the uncompensated angle has already been calculated using Equation 3. Compensation is available as an option on all Jewell Instruments electrolytic digital tiltmeters and may also be built into spreadsheets and user-defined programs.

Angle Conversion Factors

1 degree = 60 arc minutes = 3600 arc seconds = 17453 µradians = 0.01745 radians
1 arc second = 4.85 microradians
1 µradian = 1 µinch per inch = 1 micron per meter = 1 mm per km

If Canada had a hinge at Winnipeg and a man standing in Vancouver lifted the west coast to chest height, he would tilt the western half of the country by 1 µradian.

Electrolytic Tiltmeter Temperature Coefficients